Matriz adjunta: Entendiendo la adjunta matriz paso a paso

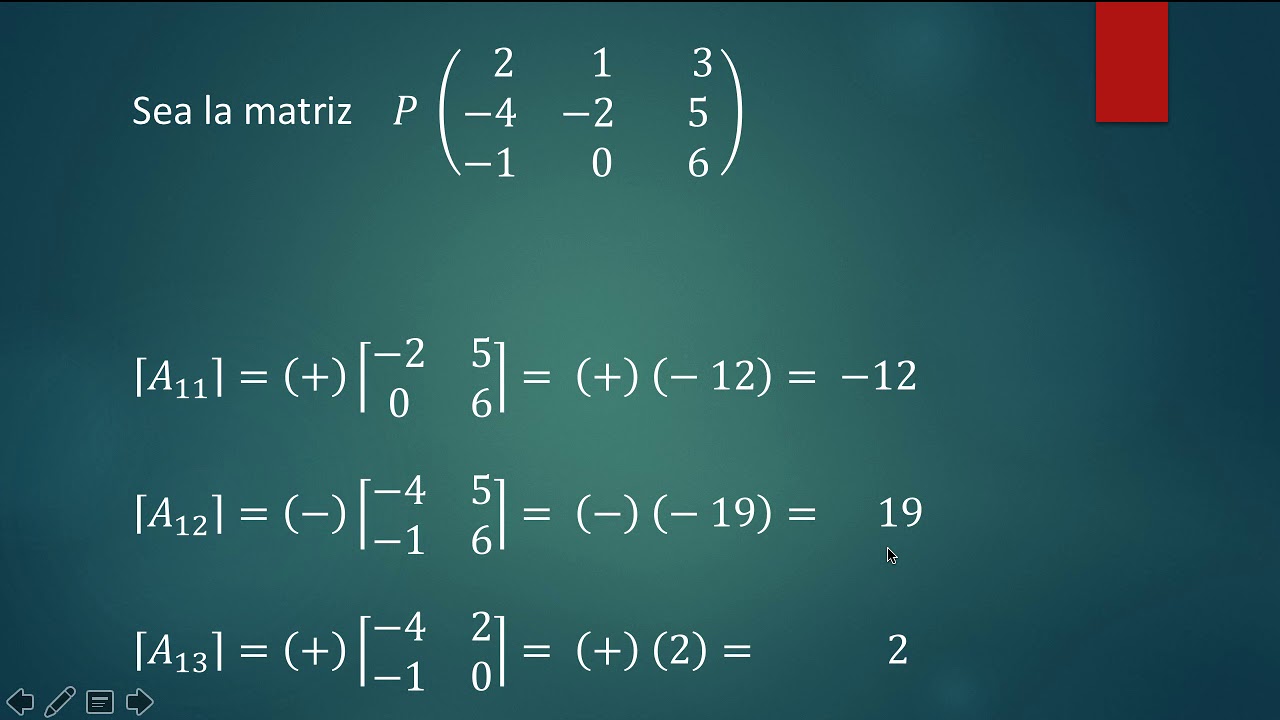
La matriz adjunta es un concepto fundamental en álgebra lineal que permite el cálculo de la inversa de una matriz. Entender su aplicación es clave para resolver sistemas de ecuaciones lineales, entre otras cuestiones matemáticas importantes.

A través de una serie de pasos claros y ejemplos prácticos, adquiriremos un conocimiento profundo sobre este tema que irá más allá de una simple definición. Si has estado buscando una guía completa para entender la adjunta matriz, has llegado al lugar indicado.

¿Qué es la Matriz Adjacente?

La matriz adjunta, a menudo denotada como adj(A), es el conjunto de todos los cofactores de una matriz, transpuestos. Esta operación es esencial en el estudio de determinantes y tiene aplicaciones directas en la computación de matrices inversas. Es importante no confundir la adjunta matriz con la matriz inversa, aunque están íntimamente relacionadas.

Importancia de la Matriz Adjacente

La matriz adjunta tiene múltiples aplicaciones en diversos campos, incluyendo la ingeniería, la física y la economía. Es utilizada, entre otras cosas, para derivar la fórmula de la inversa de una matriz y en el cálculo de determinantes de matrices cuadradas. Sin esta herramienta, se complicaría realizar operaciones más avanzadas en álgebra lineal.

Propiedades de la Matriz Adjacente

• Transposición: La adjunta matriz se obtiene mediante la transposición de la matriz de cofactores.
• Determinante: El determinante de una matriz y el determinante de su matriz adjunta están conectados de manera que el determinante de la adjunta matriz es igual al determinante de la matriz elevada a la potencia de (n-1), donde n es el tamaño de la matriz.
• Inversa: La relación entre la matriz adjunta y la inversa de una matriz es crucial, ya que la inversa de una matriz puede ser calculada utilizando la adjunta matriz.

Paso 1: Definición de la Matriz Original

El primer paso para obtener una matriz adjunta es definir la matriz original. Esta debe ser una matriz cuadrada, es decir, tener el mismo número de filas y columnas. Por ejemplo, consideremos la matriz A:

A = | 1  2  3 |
    | 0  1  4 |
    | 5  6  0 |

Asegúrate de que tu matriz sea cuadrada, ya que la adjunta matriz solo se puede calcular para matrices de este tipo.

Paso 2: Cálculo de los Menores

En este paso, debemos calcular los menores de cada elemento de la matriz original. Un menor es el determinante de la submatriz que se obtiene al eliminar la fila y la columna del elemento considerado. Para la matriz A dada, calculamos los menores:

• M_{11} = Determinante de | 1 4 | = (1*0 – 4*6) = -24
• M_{12} = Determinante de | 0 4 | = (0*0 – 4*5) = -20
• M_{13} = Determinante de | 0 1 | = (0*6 – 1*5) = -5
• M_{21} = Determinante de | 2 3 | = (2*0 – 3*6) = -18
• M_{22} = Determinante de | 1 4 | = 1*0 – 4*5 = -20
• M_{23} = Determinante de | 1 2 | = 1*6 – 2*5 = -4
• M_{31} = Determinante de | 2 3 | = (2*4 – 3*1) = 5
• M_{32} = Determinante de | 1 4 | = (1*2 – 3*0) = 2
• M_{33} = Determinante de | 1 2 | = (1*1 – 2*0) = 1

Estos menores son fundamentales para calcular la matriz adjunta en el siguiente paso.

Paso 3: Transposición de la Matriz de Menores

Una vez que hemos calculado los menores, el siguiente paso es formar la matriz de cofactores usando los menores. Luego, transpondremos esta matriz. Por ejemplo, si los menores calculados se disponen en una matriz:

M = | -24 -20 -5  |
    | -18 -20 -4  |
    |  5   2  1  |

La matriz de cofactores cambiará según los signos de los menores. La transposición implica cambiar filas por columnas:

C = | -24  -18  5  |
    | -20  -20  2  |
    | -5   -4   1  |

Paso 4: Aplicación de la Fórmula de la Matriz Adjunta

Finalmente, aplicamos la fórmula para obtener la matriz adjunta a partir de la matriz de cofactores. La matriz adjunta se define formalmente como:

adj(A) = C^T

Donde C es la matriz de cofactores. Ahora aplicamos la transposición que realizamos anteriormente:

adj(A) = | -24  -20  -5  |
          | -18  -20  2  |
          |  5   -4   1  |

Ejemplos Prácticos

Vamos a ver más ejemplos prácticos de cálculo de la matriz adjunta. Considérate que trabajas con matrices más pequeñas y luego, si es necesario, abordas matrices más grandes. Por ejemplo, podemos considerar una matriz 2×2:

B = | a  b  |
    | c  d  |

La matriz adjunta de B se puede calcular utilizando la regla:

adj(B) = | d -b |
         | -c a |

Así, puedes aplicar lo aprendido en matrices más simples y ver cómo se puede extender a matrices más complejas. Recomendamos que practiques con diferentes matrices y valores para afianzar tu comprensión.

Errores Comunes y Cómo Evitarlos

Al trabajar con la matriz adjunta, es normal cometer algunos errores. Aquí te detallamos algunos de los más comunes y cómo evitarlos:

• Confundir menores con cofactores: Recuerda que los cofactores son los menores multiplicados por (-1) elevado a la suma de los índices de fila y columna.
• Error en la transposición: Verifica que hayas cambiado filas por columnas correctamente.
• Determinar incorrectamente el determinante: Asegúrate de que los cálculos de los determinantes de las submatrices sean precisos.

Conclusión

La matriz adjunta es una herramienta esencial en álgebra lineal, necesaria para comprender mejor las propiedades y las operaciones de matrices. A través de los pasos que hemos analizado, puedes fácilmente calcular la adjunta matriz y aplicar este conocimiento en diversas áreas de las matemáticas y la física.

Recursos Adicionales para Ampliar Conocimientos

Para aquellos interesados en profundizar aún más en el tema de la matriz adjunta, te recomendamos los siguientes recursos:

• Libros de Texto: «Álgebra Lineal y sus Aplicaciones» de David C. Lay.
• Cursos en Línea: Plataformas como Coursera y edX ofrecen cursos gratuitos sobre álgebra lineal.
• Videos Educativos: Canales de YouTube como 3Blue1Brown y Khan Academy explican conceptos de álgebra lineal de manera visual.

Esperamos que esta guía te haya sido de ayuda para entender a fondo la adjunta matriz y su cálculo. La práctica continua es clave para dominar este tópico en álgebra lineal.